|
STEREONET UYGULAMALARI |
 |
|
9-Kıvrım Ekseninin Bulunması
Arazide ölçülen tabaka,
klivaj gibi ölçümler stereonette değerlendirilerek, bir
bölgedeki kıvrım ekseni belirlenebilir. Bunun için
β- veya Π- diyagramları hazırlanır
β-diyagramı
hazırlanırken düzlemlerin kendisi işaretlenir. Düzlemlerin
kesişimi kıvrım eksenini verecektir.
Π-
diyagramı yapılırken düzlemlerin kutup noktası işaretlenir
ve kutup noktaları analiz edilerek kıvrım ekseninin gidişi
belirlenir. |
|
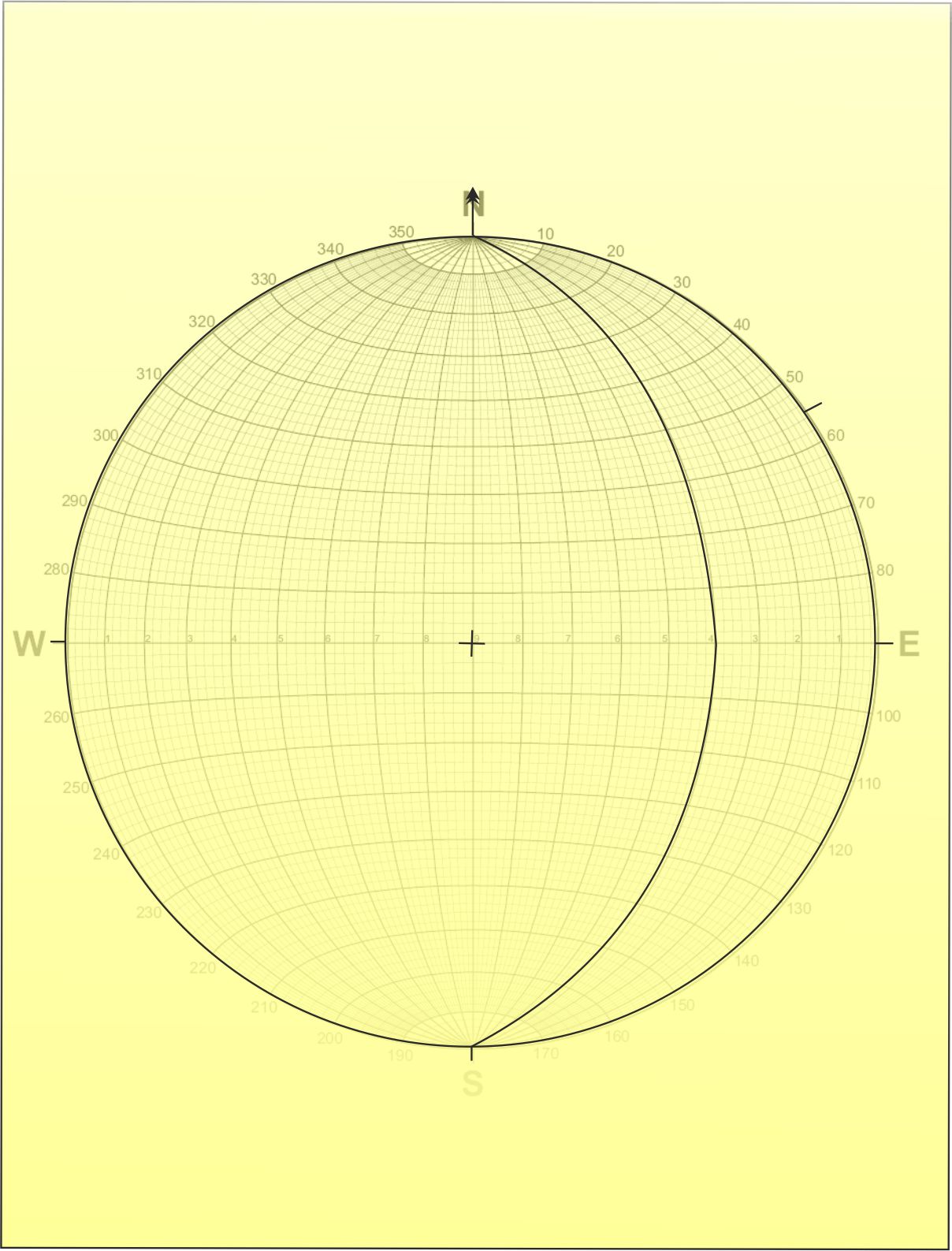
β-diyagramı
Ölçüm sayısı fazla değilse β-diyagramı yapılır.
β-diyagramının hazırlanması, Π- diyagramına göre daha fazla
zaman alır ve yorumu daha karışıktır. β-diyagramı
hazırlanırken ölçümlerin konumlarına göre yayları çizilir ve
bu düzlemlere ilişkin yayların kesişim noktaları bulunur.
Tabakalar ortalama bir kıvrım ekseni boyunca kesişeceklerdir |
 |
Problem. Kıvrımlı bir bölgede aşağıda
verilen tabaka ölçümleri alınmıştır. Bu ölçümleri
β-diyagramı yaparak değerlendiriniz
K-G, 40D
K20D,
77GD
K35D,
62KB
K55D,
34 KB
K65D,
24KB
K85D,
20 KB
K30B,
24KD
K24D,
90
K12D,
60GD
K48B,
18 KD
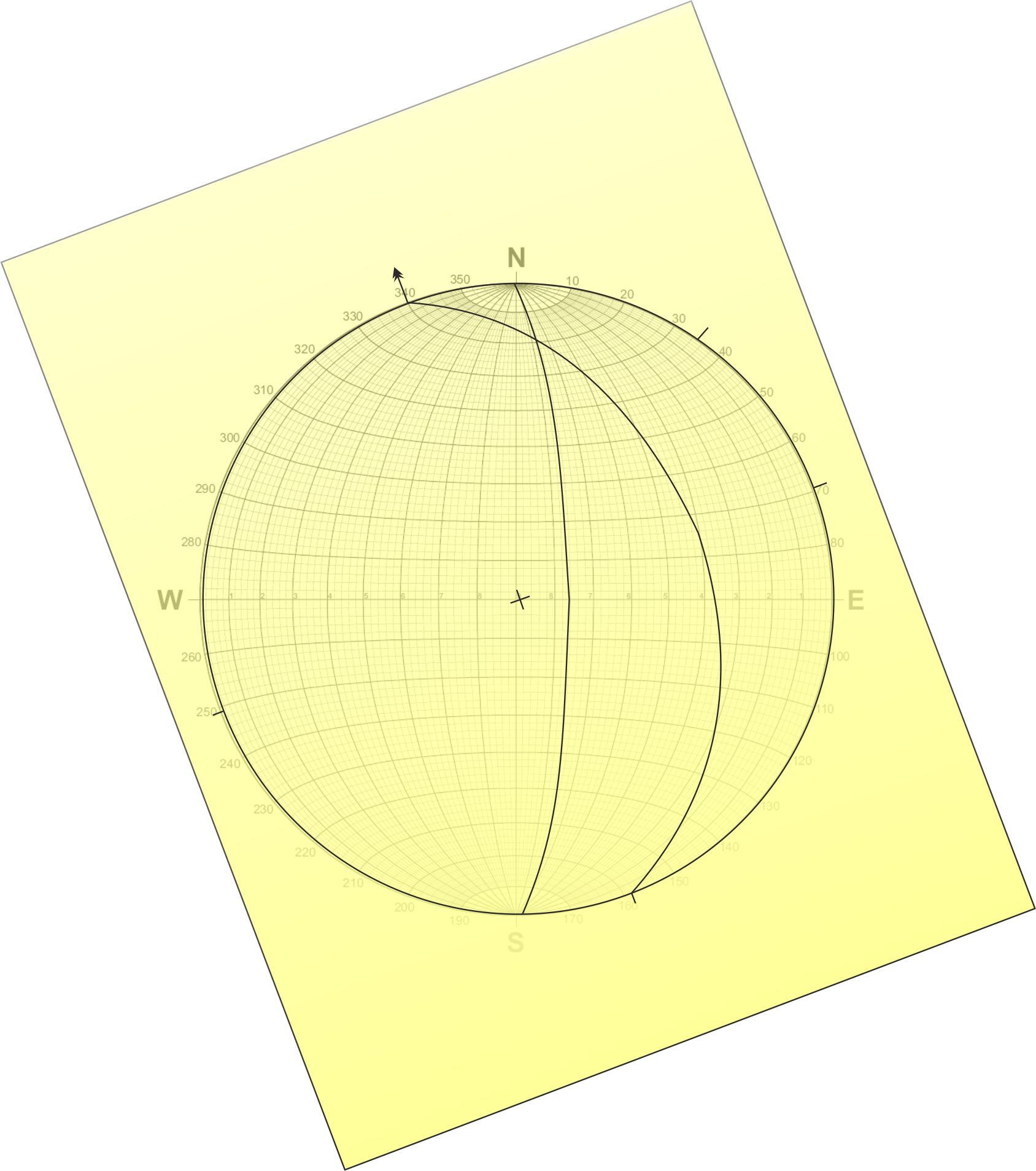
Çözüm
1: Sırasıyla tek tek tabaka düzlemleri işaretlenir (İşaretlenen
K-G, 40D)
|
 |
2- İşaretlenen ikinci ölçüm
|
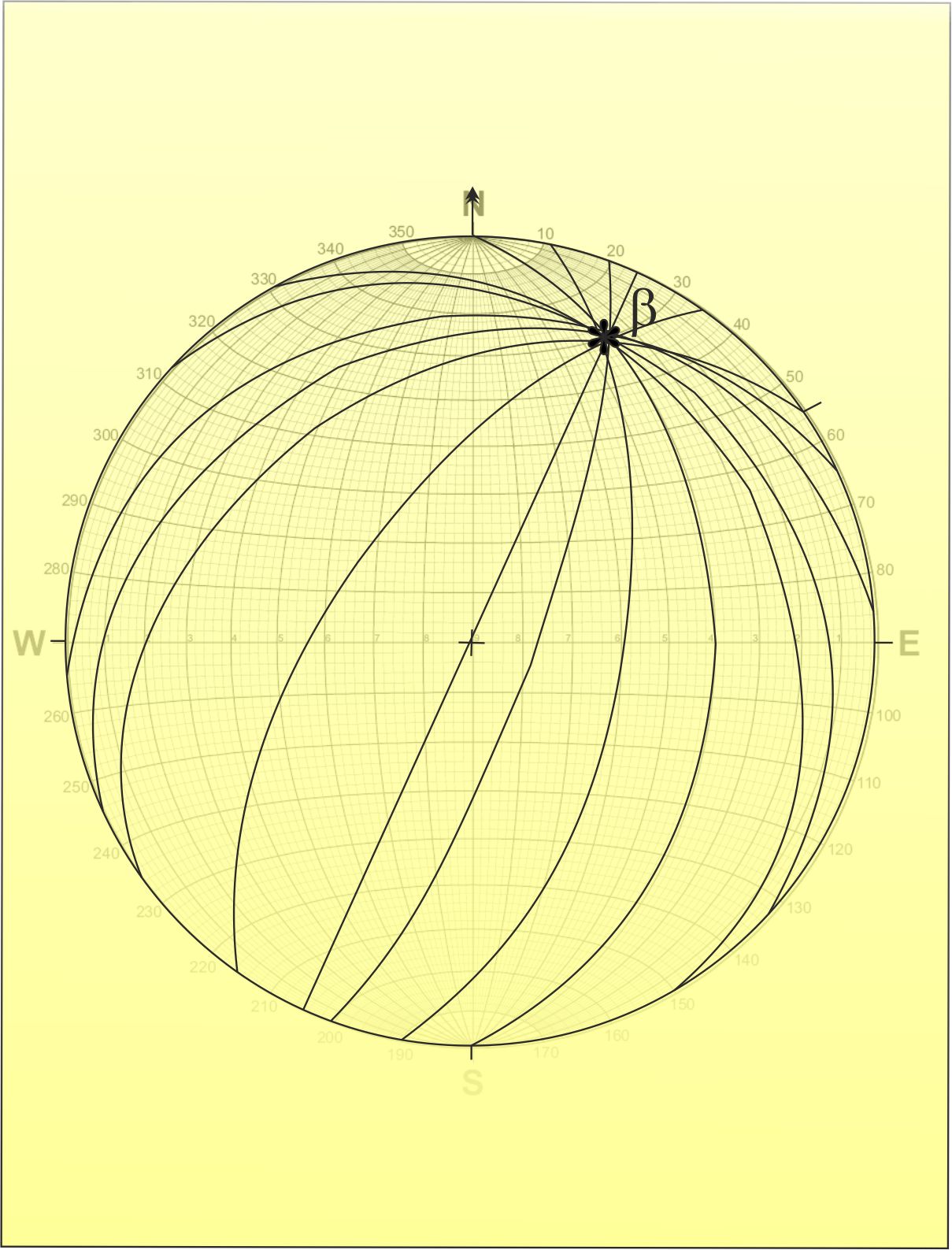 |
3-Tüm tabaka düzlemleri işaretlenir. Tabaka düzlemleri bir
noktada kesişecektir. Bu nokta
(β-)
kıvrım eksenidir.
NOT:
Buradaki örnek ideal bir örnektir. Genellikle düzlemler bir
noktada değil bir alan boyunca yoğunlaşacak şekilde kesişirler.
Bu durumda gözle veya arakesit noktaları konturlanarak egemen
kıvrım ekseni gidişi bulunur |
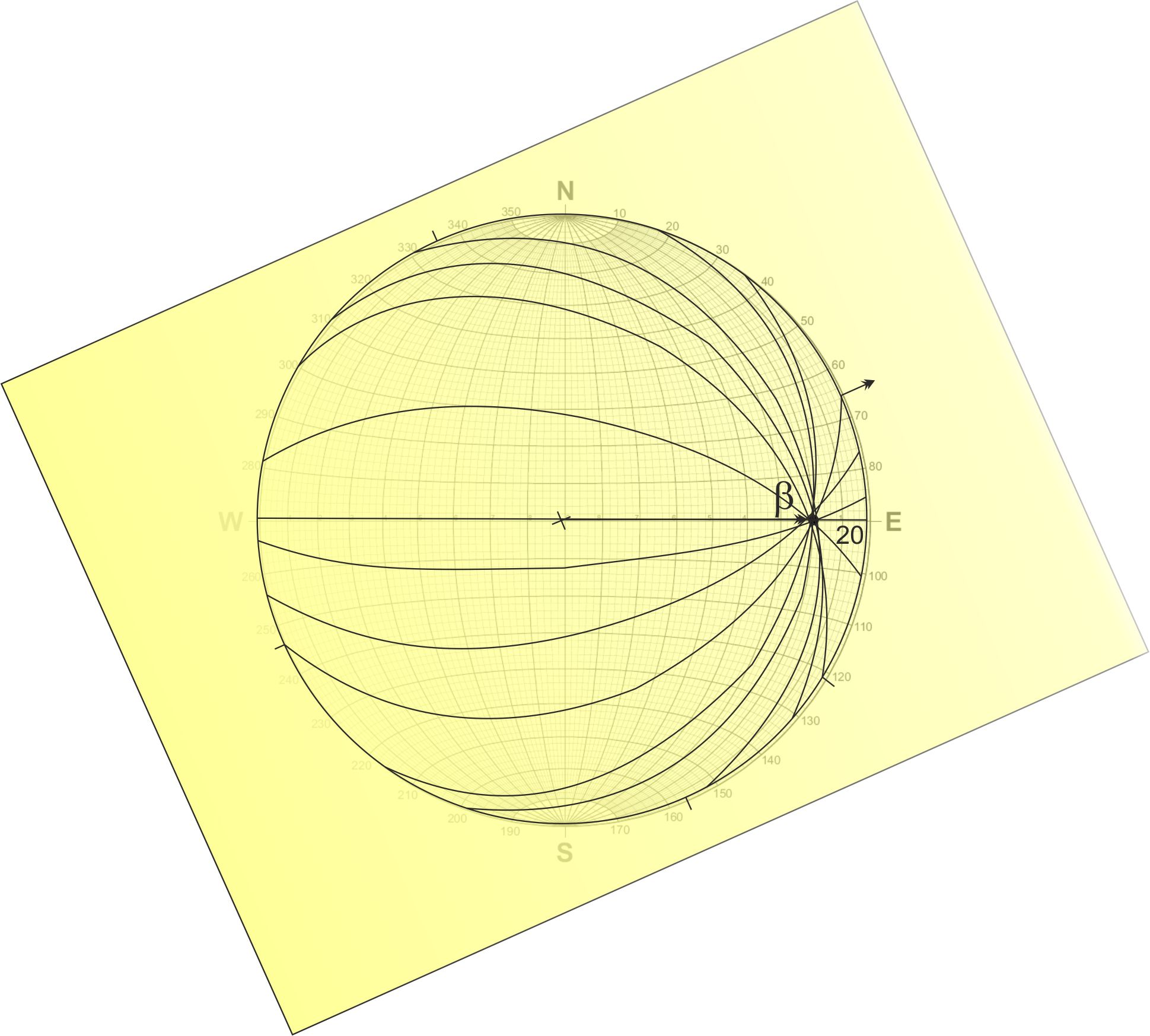 |
4- Belirlenen kıvrım ekseni alttaki ağın D-B eksenine
çakıştırılır. Dıştan içe doğru okunan açı (20) kıvrım ekseninin
dalım açısıdır. Noktanın şeffaf kağıt üstünde arasında bulunduğu
yön (KD) kıvrım ekseninin dalım yönüdür. |
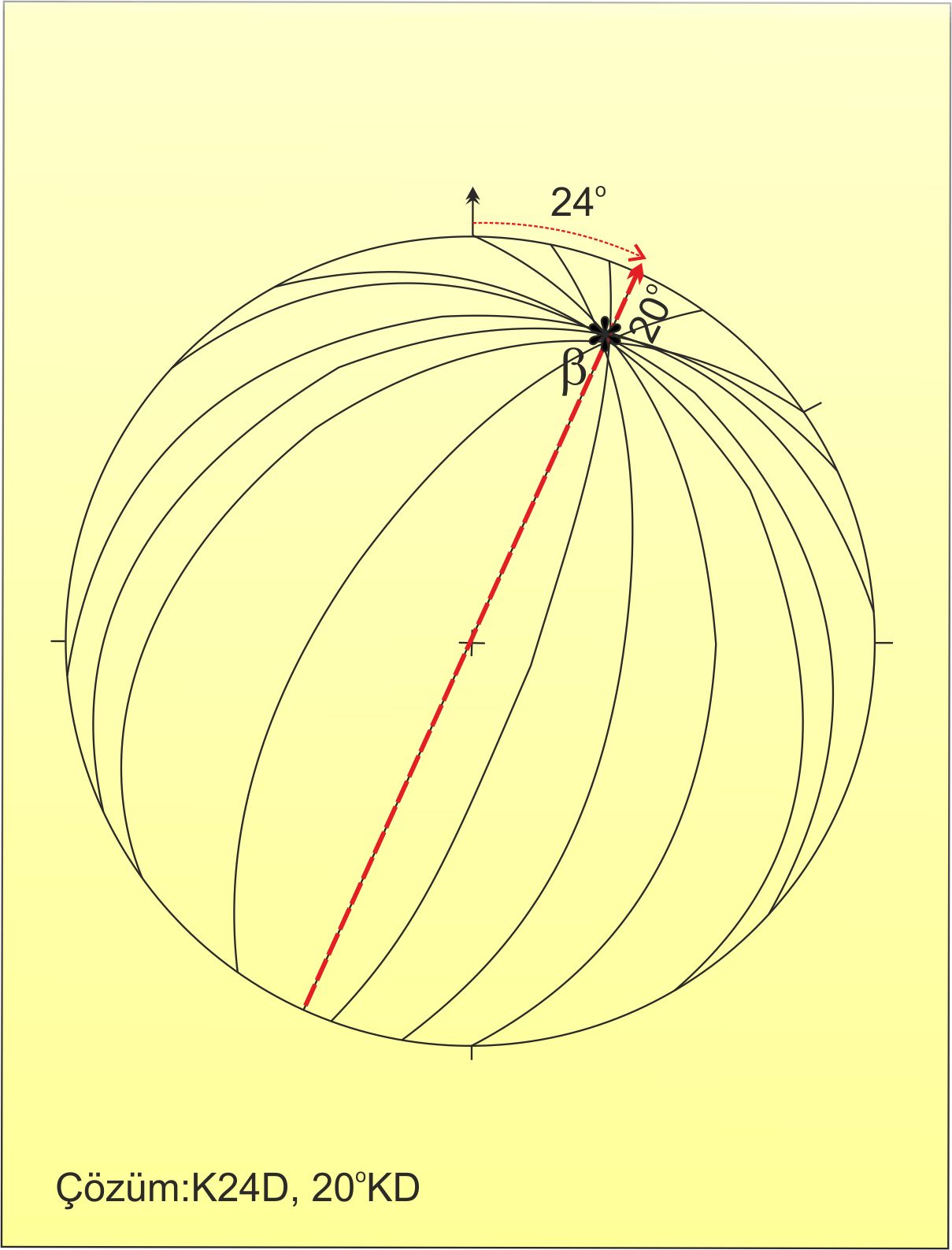 |
5-Çizgiselliğin K yönü ile ağın dış çemberi üzerinde
yaptığı dar açı (24) ise kıvrım ekseninin yönelimini verir. |
|
|
|
|
|
|
|
|
|
|
GERİ (BACK) |


